Структуры со ссылками на себя
Предположим, что мы хотим решить более общую задачу - написать программу, подсчитывающую частоту встречаемости для любых слов входного потока. Так как список слов заранее не известен, мы не можем предварительно упорядочить его и применить бинарный поиск. Было бы неразумно пользоваться и линейным поиском каждого полученного слова, чтобы определять, встречалось оно ранее или нет - в этом случае программа работала бы слишком медленно. (Более точная оценка: время работы такой программы пропорционально квадрату количества слов.) Как можно организовать данные, чтобы эффективно справиться со списком произвольных слов?
Один из способов - постоянно поддерживать упорядоченность уже полученных слов, помещая каждое новое слово в такое место, чтобы не нарушалась имеющаяся упорядоченность. Делать это передвижкой слов в линейном массиве не следует, - хотя бы потому, что указанная процедура тоже слишком долгая. Вместо этого мы воспользуемся структурой данных, называемой бинарным деревом.
В дереве на каждое отдельное слово предусмотрен "узел", который содержит:
- указатель на текст слова; - счетчик числа встречаемости; - указатель на левый сыновний узел; - указатель на правый сыновний узел.
У каждого узла может быть один или два сына, или узел вообще может не иметь сыновей.
Узлы в дереве располагаются так, что по отношению к любому узлу левое поддерево содержит только те слова, которые лексикографически меньше, чем слово данного узла, а правое - слова, которые больше него. Вот как выглядит дерево, построенное для фразы "now is the time for all good men to come to the aid of their party" ("настало время всем добрым людям помочь своей партии"), по завершении процесса, в котором для каждого нового слова в него добавлялся новый узел:
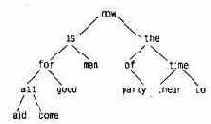
Чтобы определить, помещено ли уже в дерево вновь поступившее слово, начинают с корня, сравнивая это слово со словом из корневого узла. Если они совпали, то ответ на вопрос — положительный. Если новое слово меньше слова из дерева, то поиск продолжается в левом поддереве, если больше, то — в правом. Если же в выбранном направлении поддерева не оказалось, то этого слова в дереве нет, а пустующая позиция, говорящая об отсутствии поддерева, как раз и есть то место, куда нужно "подвесить" узел с новым словом. Описанный процесс по сути рекурсивен, так как поиск в любом узле использует результат поиска в одном из своих сыновних узлов. В соответствии с этим для добавления узла и печати дерева здесь наиболее естественно применить рекурсивные функции.
Вернемся к описанию узла, которое удобно представить в виде структуры с четырьмя компонентами:
struct tnode { /* узел дерева */ char *word; /* указатель на текст */ int count; /* число вхождений */ struct tnode *left; /* левый сын */ struct tnode *right; /* правый сын */ };
Приведенное рекурсивное определение узла может показаться рискованным, но оно правильное. Структура не может включать саму себя, но ведь
struct tnode *left;
объявляет left как указатель на tnode, а не сам tnode.
Иногда возникает потребность во взаимоссылающихся структурах: двух структурах, ссылающихся друг на друга. Прием, позволяющий справиться с этой задачей, демонстрируется следующим фрагментом:
struct t { ... struct s *p; /* р указывает на s */ }; struct s { ... struct t *q; /* q указывает на t */ }
Вся программа удивительно мала - правда, она использует вспомогательные программы вроде getword, уже написанные нами. Главная программа читает слова с помощью getword и вставляет их в дерево посредством addtree.
#include <stdio.h> #include <ctype.h> #include <string.h>
#define MAXWORD 100
struct tnode *addtree(struct tnode *, char *); void treeprint(struct tnode *); int getword(char *, int);
/* подсчет частоты встречаемости слов */ main() { struct tnode *root; char word[MAXWORD];
root = NULL; while (getword (word, MAXWORD) != EOF) if (isalpha(word[0])) root = addtree(root, word); treeprint(root); return 0; }
Функция addtree рекурсивна. Первое слово функция main помещает на верхний уровень дерева (корень дерева). Каждое вновь поступившее слово сравнивается со словом узла и "погружается" или в левое, или в правое поддерево с помощью рекурсивного обращения к addtree. Через некоторое время это слово обязательно либо совпадет с каким-нибудь из имеющихся в дереве слов (в этом случае к счетчику будет добавлена 1), либо программа встретит пустую позицию, что послужит сигналом для создания нового узла и добавления его к дереву. Создание нового узла сопровождается тем, что addtree возвращает на него указатель, который вставляется в узел родителя.
struct tnode *talloc(void); char *strdup(char *);
/* addtree: добавляет узел со словом w в р или ниже него */ struct tnode *addtree(struct tnode *p, char *w) { int cond;
if (р == NULL) { /* слово встречается впервые */ p = talloc(); /* создается новый узел */ p->word = strdup(w); p->count = 1; p->left = p->right = NULL; } else if ((cond = strcmp(w, p->word)) == 0) p->count++; /* это слово уже встречалось */ else if (cond < 0) /* меньше корня левого поддерева */ p->left = addtree(p->left, w); else /* больше корня правого поддерева */ p->right = addtree(p->right, w); return p; }
Память для нового узла запрашивается с помощью программы talloc, которая возвращает указатель на свободное пространство, достаточное для хранения одного узла дерева, а копирование нового слова в отдельное место памяти осуществляется с помощью strdup. (Мы рассмотрим эти программы чуть позже.) В тот (и только в тот) момент, когда к дереву подвешивается новый узел, происходит инициализация счетчика и обнуление указателей на сыновей. Мы опустили (что неразумно) контроль ошибок, который должен выполняться при получении значений от strdup и talloc.
Функция treeprint печатает дерево в лексикографическом порядке: для каждого узла она печатает его левое поддерево (все слова, которые меньше слова данного узла), затем само слово и, наконец, правое поддерево (слова, которые больше слова данного узла).
/* treeprint: упорядоченная печать дерева р */ void treeprint(struct tnode *p) { if (p != NULL) { treeprint (p->left); printf("%4d %s\n", p->count, p->word); treeprint(p->right); } }
Если вы не уверены, что досконально разобрались в том, как работает рекурсия, "проиграйте" действия treeprint на дереве, приведенном выше. Практическое замечание: если дерево "несбалансировано" (что бывает, когда слова поступают не в случайном порядке), то время работы программы может сильно возрасти. Худший вариант, когда слова уже упорядочены; в этом случае затраты на вычисления будут такими же, как при линейном поиске. Существуют обобщения бинарного дерева, которые не страдают этим недостатком, но здесь мы их не описываем.
Прежде чем завершить обсуждение этого примера, сделаем краткое отступление от темы и поговорим о механизме запроса памяти. Очевидно, хотелось бы иметь всего лишь одну функцию, выделяющую память, даже если эта память предназначается для разного рода объектов. Но если одна и та же функция обеспечивает память, скажем) и для указателей на char, и для указателей на struct tnode, то возникают два вопроса. Первый: как справиться с требованием большинства машин, в которых объекты определенного типа должны быть выровнены (например, int часто должны размещаться, начиная с четных адресов)? И второе: как объявить функцию-распределитель памяти, которая вынуждена в качестве результата возвращать указатели разных типов?
Вообще говоря, требования, касающиеся выравнивания, можно легко выполнить за счет некоторого перерасхода памяти. Однако для этого возвращаемый указатель должен быть таким, чтобы удовлетворялись любые ограничения, связанные с выравниванием. Функция alloc, описанная в , не гарантирует нам любое конкретное выравнивание, поэтому мы будем пользоваться стандартной библиотечной функцией malloc, которая это делает. В мы покажем один из способов ее реализации.
Вопрос об объявлении типа таких функций, как malloc, является камнем преткновения в любом языке с жесткой проверкой типов. В Си вопрос решается естественным образом: malloc объявляется как функция, которая возвращает указатель на void. Полученный указатель затем явно приводится к желаемому типу (Замечание о приведении типа величины, возвращаемой функцией malloc, нужно переписать. Пример коpректен и работает, но совет является спорным в контексте стандартов ANSI/ISO 1988-1989 г. На самом деле это не обязательно (при условии что приведение void* к ALMOSTANYTYPE* выполняется автоматически) и возможно даже опасно, если malloc или ее заместитель не может быть объявлен как функция, возвращающая void*. Явное приведение типа может скрыть случайную ошибку. В другие времена (до появления стандарта ANSI) приведение считалось обязательным, что также справедливо и для C++. — Примеч. авт.). Описания malloc и связанных с ней функций находятся в стандартном заголовочном файле <stdlib.h>. Таким образом, функцию talloc можно записать так:
#include <stdlib.h>
/* talloc: создает tnode */ struct tnode *talloc(void) { return (struct tnode *) malloc(sizeof(struct tnode)); }
Функция strdup просто копирует строку, указанную в аргументе, в место, полученное с помощью malloc:
char *strdup(char *s) /* делает дубликат s */ { char *p;
p = (char *) malloc(strlen(s)+1); /* +1 для '\0' */ if (p != NULL) strcpy(p, s); return p; }
Функция malloc возвращает NULL, если свободного пространства нет; strdup возвращает это же значение, оставляя заботу о выходе из ошибочной ситуации вызывающей программе.
Память, полученную с помощью malloc, можно освободить для повторного использования, обратившись к функции free (см. и ).
Упражнение 6.2. Напишите программу, которая читает текст Си-программы и печатает в алфавитном порядке все группы имен переменных, в которых совпадают первые 6 символов, но последующие в чем-то различаются. Не обрабатывайте внутренности закавыченных строк и комментариев. Число 6 сделайте параметром, задаваемым в командной строке.
Упражнение 6.3. Напишите программу печати таблицы "перекрестных ссылок", которая будет печатать все слова документа и указывать для каждого из них номера строк, где оно встретилось. Программа должна игнорировать "шумовые" слова, такие как "и", "или" и пр.
Упражнение 6.4. Напишите программу, которая печатает весь набор различных слов, образующих входной поток, в порядке возрастания частоты их встречаемости. Перед каждым словом должно быть указано число вхождений.
